AREA SOMBREADA

                                                                   CUADRADO

El cuadrado es una figura geométrica que pertenece a los paralelogramos porque tiene 4 lados.

Los 4 lados miden lo mismo y son paralelos dos a dos. ¿Esto que quiere decir? Que tiene 2 lados paralelos entre sí, y los otros 2 también son paralelos entre sí.

Los 4 ángulos internos de un cuadrado miden 90º, es decir, son ángulos rectos. La suma de los 4 ángulos internos es de 360º.

Los 4 ángulos externos miden 270º.

Las dos diagonales que tienen son iguales y el punto donde se cortan las dos diagonales es el centro de simetría del cuadrado.

La fórmula para obtener el área del cuadrado es:
Área = base por altura

A = b x h

O puedes utilizar la fórmula:
Área = lado al cuadrado

Área = L²

Ejemplo:

Con la primera fórmula queda así.

A = b x h
A = 3 x 3
A = 9 cm²

Y con la segunda fórmula así

A = L²
A = 3²
A = 3 x 3

A = 9 cm²                    


                                                       CIRCULO     

      El círculo es una figura geométrica que se realiza trazando una curva que está siempre a la misma distancia de un punto que llamamos centro.

A continuación vamos a ver las distintas partes del círculo.

                                                  

                                                             

Centro:

El centro del círculo (o centro de la circunferencia, mejor dicho) es el punto del cual equidistan todos los puntos.

Radio:

El radio es un segmento del círculo que une el centro con cualquier punto de la circunferencia.

Diámetro:

El diámetro es un segmento del círculo que une dos puntos de la circunferencia pasando por el centro y lo divide en dos partes iguales. El diámetro es dos veces el radio, o lo que es lo mismo, el radio es la mitad del diámetro.

                                                 

                                             

Cuerda:

La cuerda es un segmento que une dos puntos de la circunferencia pero lo que le diferencia del diámetro es que no pasa por el centro del círculo. Por tanto, la cuerda siempre será más corta que el diámetro.

                                              

El área de un círculo con radio r > 0 es

Recordad que π es el número pi. Como este número tiene infinitos decimales, escribiremos una aproximación: π = 3,14.

EJEMPLO.

Necesitamos hallar el radio r del círculo. Observando la figura, el diámetro es d = 1cm . Como el radio es dos veces el diámetro, el radio es r = 0,5cm.

Ahora ya podemos calcular el área del círculo:

                                                                   EJERCICIOS


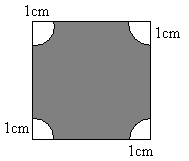
CALCULAR EL AREA SOMBREADA DE LAS SIGUIENTES FIGURAS:


1.



2.